Analyse stochastischer Prozesse

Schwingungen des Glockenläutens der Marienkirche NB klein

Hauptgegenstand der Analyse stochastischer Prozesse ist die Untersuchung sogenannter Zeitreihen. Eine Zeitreihe ist eine (zeitlich) geordnete Folge von Daten (Beobachtungen) zu diskreten Zeitpunkten.

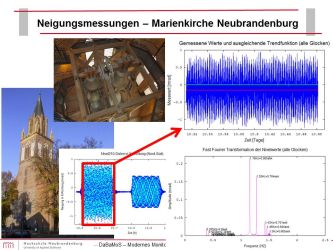
Heutzutage liegen messtechnisch erfasste Daten durch automatisierte Ziel- und Abgriffsysteme oft mit konstantem zeitlichem Abstand Δt vor, weshalb manche Autoren bei einer Zeitreihe auch von einer „digitalen Realisierung eines mathematischen Prozesses“ sprechen. Für manche Algorithmen ist das Vorliegen zeitlich äquidistanter Daten eine Voraussetzung. Andere Auswertetechniken, die z.T. auf der Ausgleichungsrechnung basieren, setzen dies nicht unbedingt voraus. In jedem Falle ist die Reihenfolge der Daten (Messwerte) einer Zeitreihe von großer Relevanz. Sukzessive Folgeglieder sind in der Regel nicht als stochastisch voneinander unabhängig zu betrachten. Aber auch gewisse physikalische Gesetzmäßigkeiten wie periodische Wiederholungen führen zu Korrelationen zwischen Messwerten in beliebigen zeitlichen Abständen. So ist leicht einzusehen, dass Messwerte, die zu gleicher Uhrzeit unter nahezu identischen Bedingungen an aufeinanderfolgenden Tagen gewonnen werden, ein ähnliches Verhalten aufzeigen, was sich dann als Periode von T = 24h in den Daten wiederspiegelt. Natürlich tauchen gewisse Periodizitäten auch in anderen, übere längere Zeiträume beobachteten physikalischen Prozessen auf. Das können sehr langsame aber auch extrem hochfrequente Bewegungen sein, wie das Beispiel des Glockenläutens an der Marienkirche zu Neubrandenburg zeigt. Solche Effekte aufzudecken ist Ziel der Zeitreihenanalyse.