(the order of projects is almost chronological and not by its relevance)
(2009-2013)
Nowadays face and
pattern detection is used in several areas as for example in
Videosystems for museums, security applications and quality
control of
materials. With this project we intend to develop and to improve
classification algorithms of high numerical efficiency
for use in object
indentification in images and object following in image sequences.
Classifiers need to separate high dimensional vectors of attributes.
Algorithms need to be robust and well structured. Support Vector
Machines satisfy those demands and give an adequate base for further
acceleration. Single approaches are sparse
approximation of SVMs, cascadation of classifications, an efficient
presentation of support vectors and effectively implemented operations.
The goal of this project is the improvement of the existing algorithms
in view to computational time, numerical efficiency, effect of
restrictions
and complexity with the goal of a flexible program library for further
use in scientific and commercial applications.
(2009-2010)
The atmospheric
boundary layer, which vertical extension is described by the
mixing layer height (MLH), plays an important role for the exchange of
heat, momentum and moisture between the surface and the free
atmosphere. The MLH is one of the key parameters for the transportat
and dispersion of air pollutants and an important input value for
dispersion models. Therefore, a lot of efforts have been undertaken
during the last decades to use ground-based remote sensing systems,
like sodar, sodar/RASS, wind profiler radar or ceilometer for a
continuous observation of the MLH.
In collaboration with JenOptik and the German
Weather Agency we aim to develop efficient algorithms for retrieving
the MLH on the basis of Ceilometer measurements.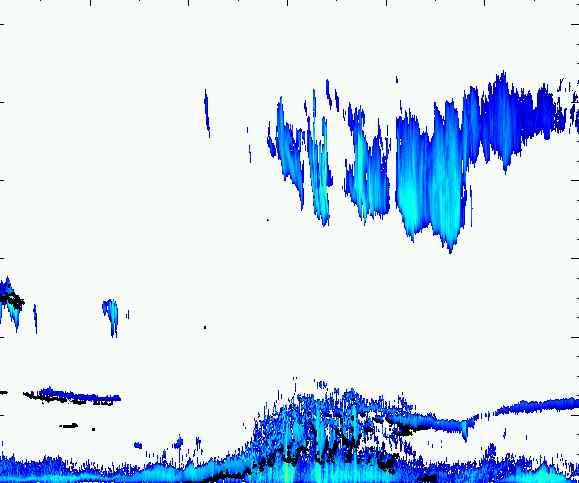
(2008-2011)
This project
aims at a thorough theory of compressed sensing for ill-posed inverse
problems. Compressed sensing is a promising new field which tries to
tackle the problem of high-dimensional data by combining the measuring
and the compression step into one single process of "compressive
sampling". It is the goal to get a proper formulation of this theory in
infinite dimensional spaces and to treat ill-posed operators - both
linear and nonlinear. Further we intend applications to the areas of
medical imaging, geo-data analysis and color image restauration.
(2007-2011)
There are many important applications, using
the theory of inverse problems, which have a nonlinear structure.
Usually,
regularization is necessary because the problem is ill-posed due to
noisy data.
While the theory of regularization methods treating linear problems in
a
Hilbert space setting is well developed, there is still a considerable
need to
improve the methods for solving nonlinear problems.
(2007-2010)
Image modelling, inpainting, decomposition and restoration by redundant representations and variational calculus
The goal of this project is the analysis of frames and their
use in numerical applications in the field of inverse problems (color
image inpainting, image restoration and decompostion). In image processing, when dealing with spaces of (special)
bounded variation functions the problem is often that the associated
PDE schemes that approximate the solution are numerically very
intensive and time consuming. It would be desirable to bypass this
drawback and to derive the solution of the image restoration problem in
some numerically thrifty way. Therefore we replace the classical
characterization of the function space of bounded variations by an
easier to handle framework, which is in our situation a frame-based
approach. This allows a simple reformulation of the image restoration
problem by means of the associated frame coefficients leading to
efficient algorithms. This project is in collaboration with R. Ramlau and M. Fornasier (RICAM, Linz).




(2007-2009)
DWD
(2006)
A new approach for target classification of Ka-band radar data
The goal of
this project is to develop a mathematical algorithm that allows on the
basis of cloud radar data a monitoring of: Depths of the cloud,
sometimes in several cloud layers; Cloud coverage (per cloud layer);
Overlap-factor of cloud layers; Characteristic droplet size; Mass
density of liquid water/ice water; Optical depth; Mass density of
drizzle, rainwater, snow; In-cloud dynamics, particularly vertical air
motion. This project is in collaboration with G. Peters (Metek GmbH in Elmshorn) and U. Görsdorf (DWD-German Weather Agency).

(since 2005)
The goal of
this project is to determine basic earthquake parameters
on the basis of a specific physical model (Okada approach or Green
function approach) that relies on GPS data input. The associated
inverse problem is ill-posed and adequate inversion techniques have to
be developed. The project is in collaboration with the A. Babeyko (Geoforschungszentrum Potsdam).
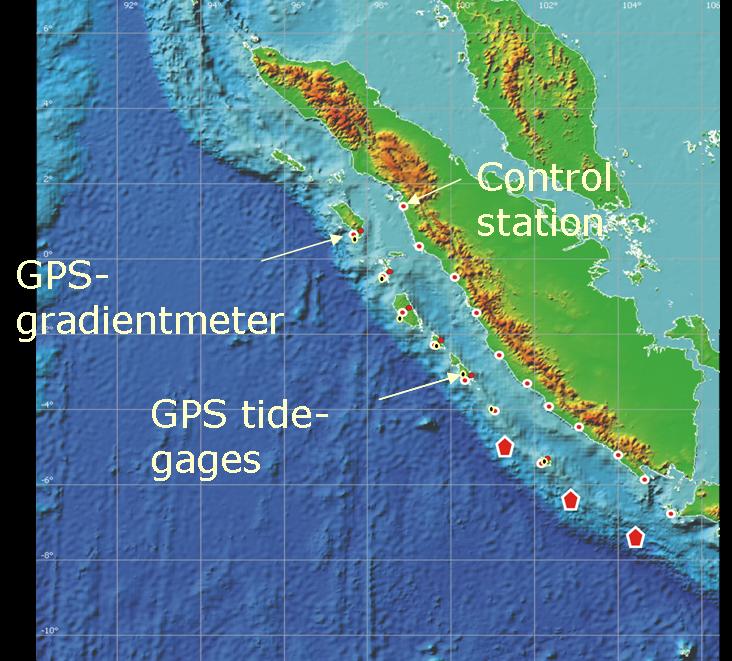
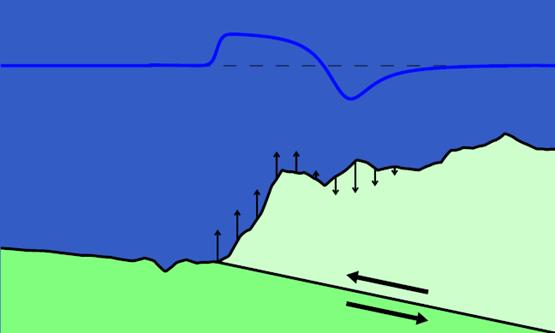
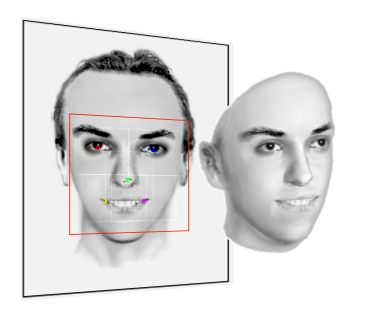
(since 2005)
Within
this project we aim to develop wavelet-based accelerated support vector
machines. The acceleration can be seen as a solution of an inverse
problem. In particular, we have to treat nonlinear problems with
sparsity constraints that lead to cascade structured very fast and
efficient classification machines. These machines are used in the
context of online face detection and 3d face modelling. In a case study
for the LKA-Berlin, we have
shown the relevance for the computation of 3d phantom images on the
basis of one single phantom skecth. This project is
in collaboration with the Prof. Vetter
(University
of Basel).
(2005-2007)
With Radar-Windprofiler
devices one can analyze the dynamics of the atmosphere. In this project
we want to make use of the relation between the measured clear air time
series and the clear air refractive index field in the associated
sampling volume. This relation is given by an special integral equation
(relating the cross covariance function with the clear air refractive
index field).
The main focus this project is the development of numerical methods that reconstruct the cross covariance function. The integral equation suggests a frame based inversion of the measured data. A direct frame reconstruction is obtained when the analyzing atoms fit with the device sampling functions. This project is in collaboration with the Prof. A. Muschinski (University of Amherst).
The main focus this project is the development of numerical methods that reconstruct the cross covariance function. The integral equation suggests a frame based inversion of the measured data. A direct frame reconstruction is obtained when the analyzing atoms fit with the device sampling functions. This project is in collaboration with the Prof. A. Muschinski (University of Amherst).
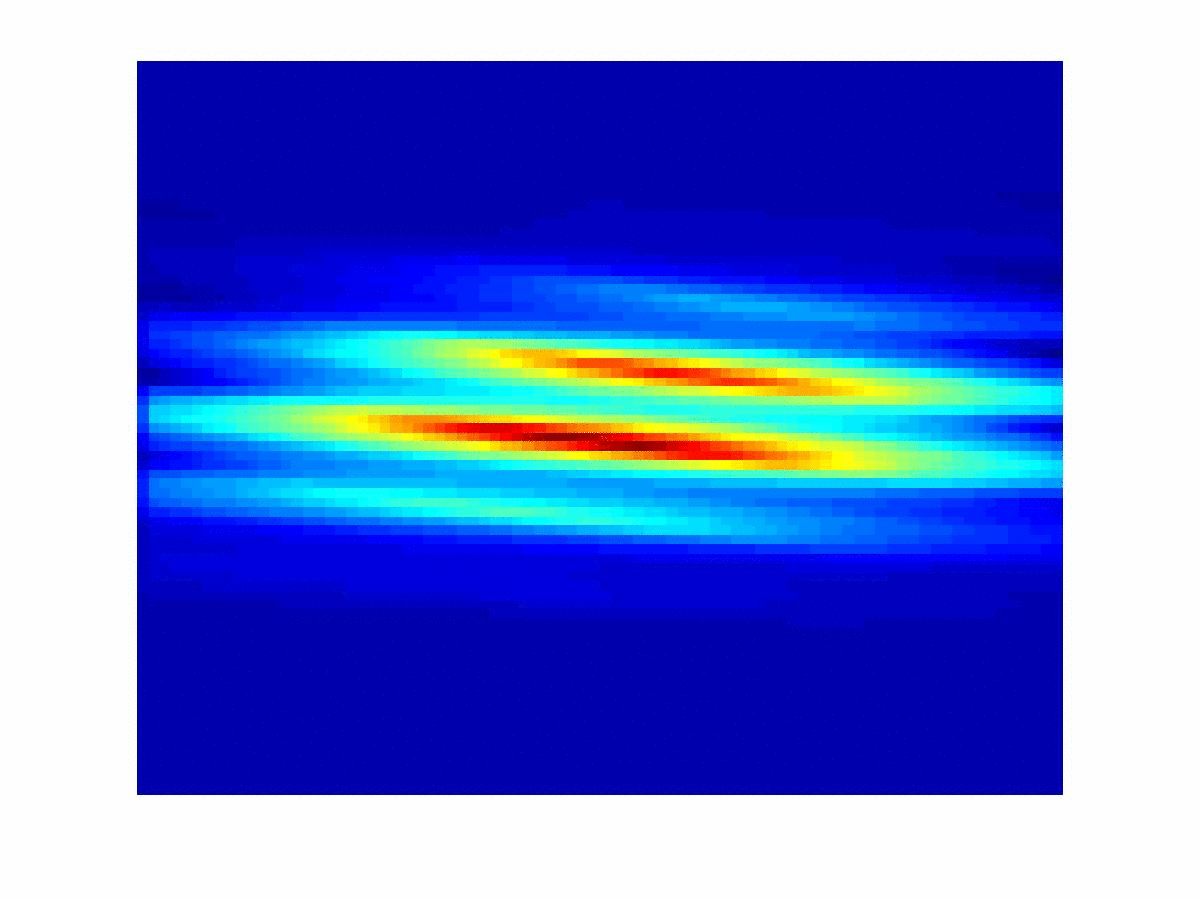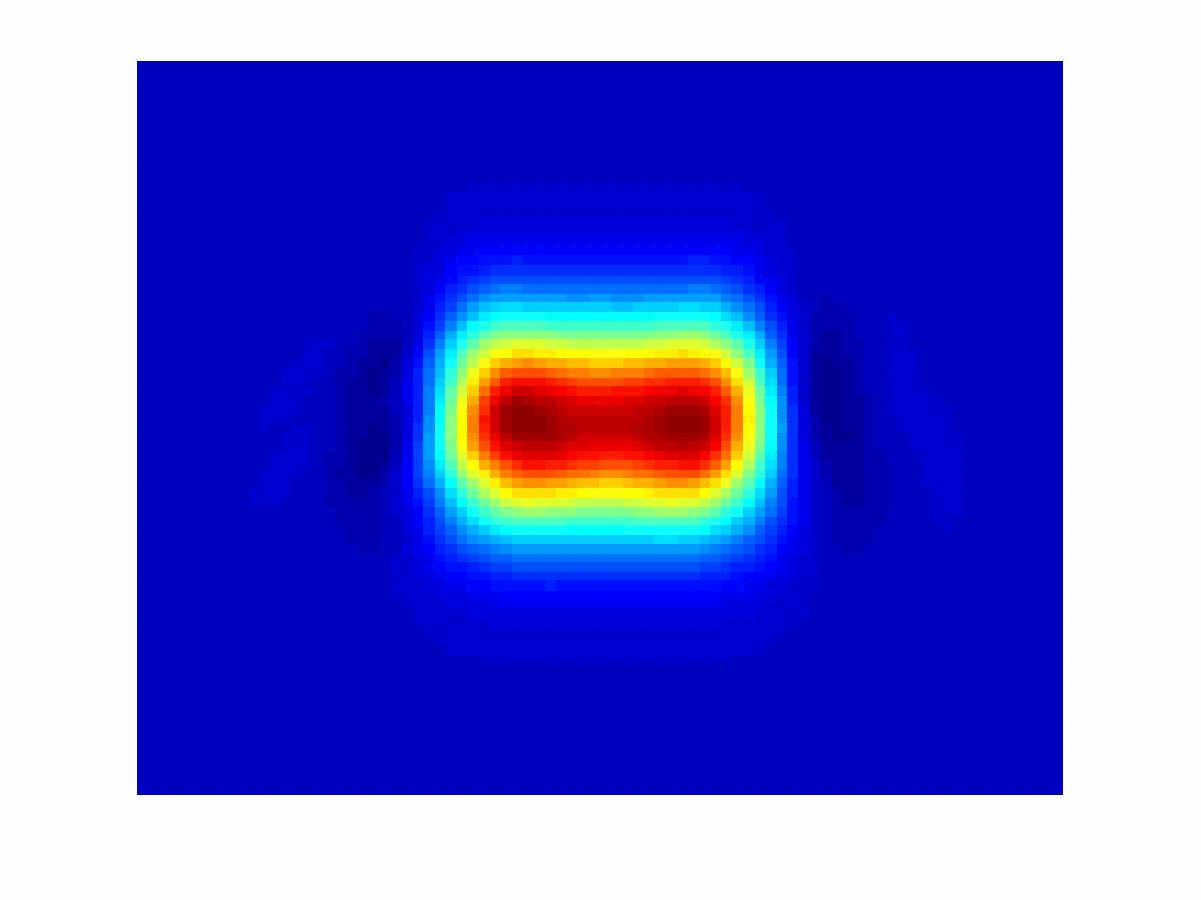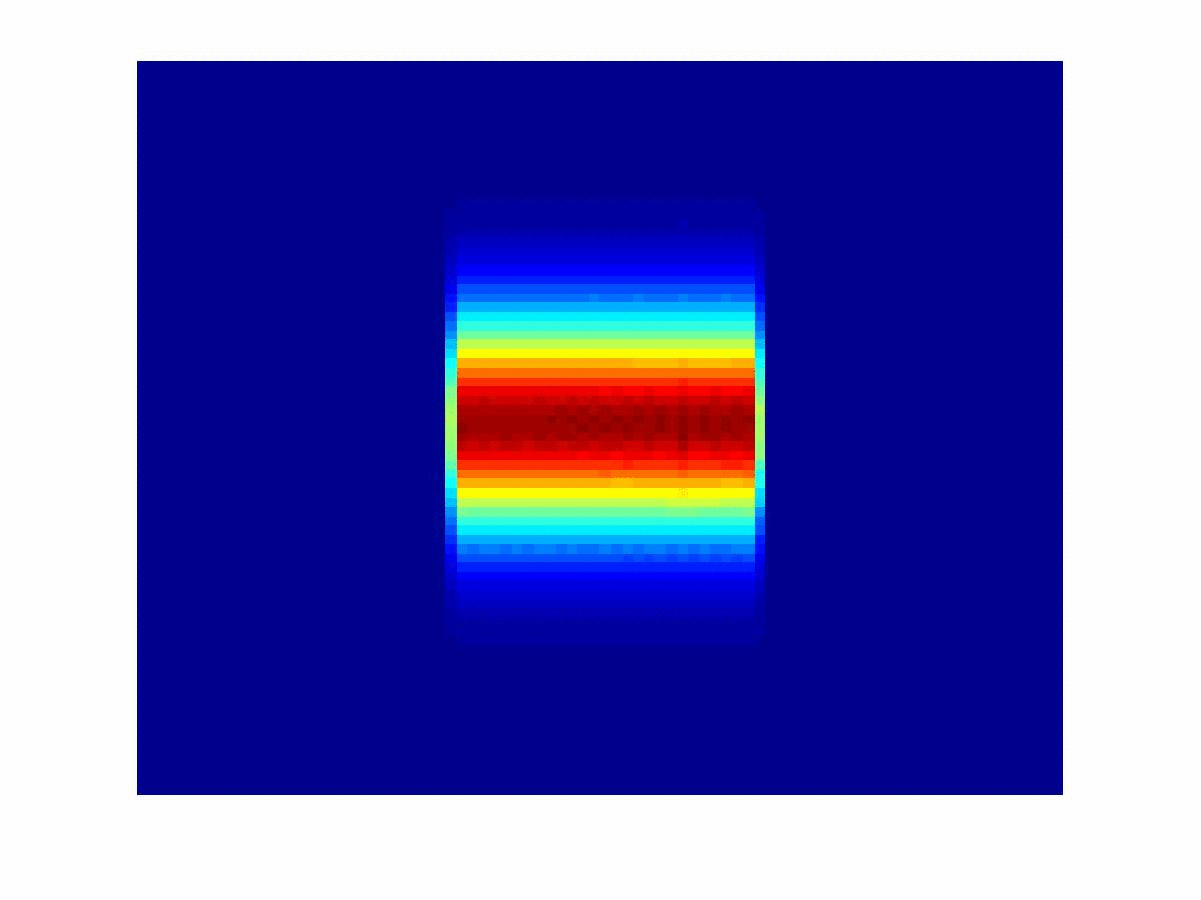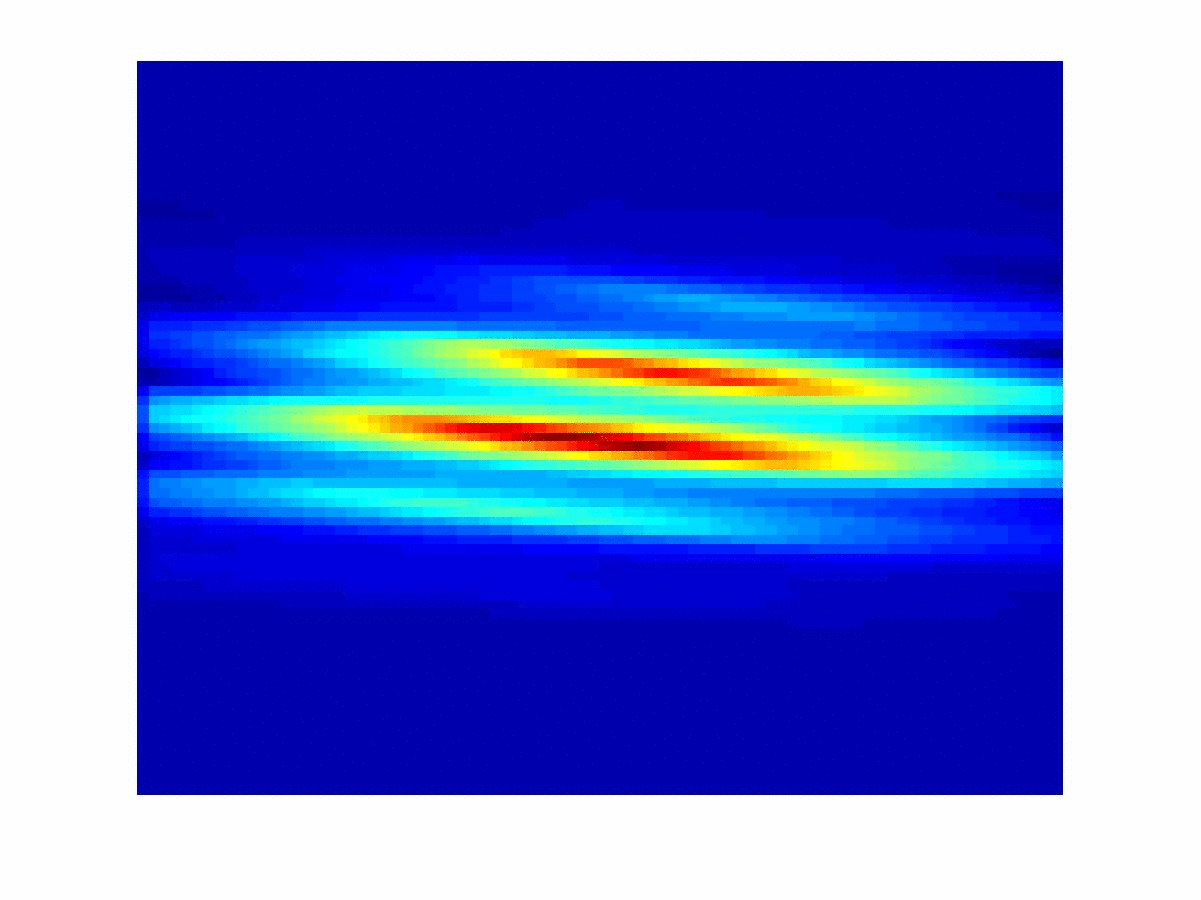
(2005-07)
In this project
we aim to develop
numerically thrifty schemes for solving operator equations in its
variational form with mixed constraints (e.g. sparsity and smoothness)
that appear in the field of image decomposition, restoration, and
classification. Sometimes it seems that wavelet bases are well suited,
sometimes frames, and sometimes it is required to go completely beyond
a ''basis''-like representation.
First experiments have shown that these techniques seem to be very well suited for texture analysis, classification problems etc. Here in this project we shall be concerned with seabed data/image restoration, i.e. a separation of the seabed pattern and the pattern caused by the ship movements made while measuring the echo of ultra sound waves transmitted down to the ocean ground. This particular application is done in collaboration with Ocean Margin Institute Bremen.
First experiments have shown that these techniques seem to be very well suited for texture analysis, classification problems etc. Here in this project we shall be concerned with seabed data/image restoration, i.e. a separation of the seabed pattern and the pattern caused by the ship movements made while measuring the echo of ultra sound waves transmitted down to the ocean ground. This particular application is done in collaboration with Ocean Margin Institute Bremen.
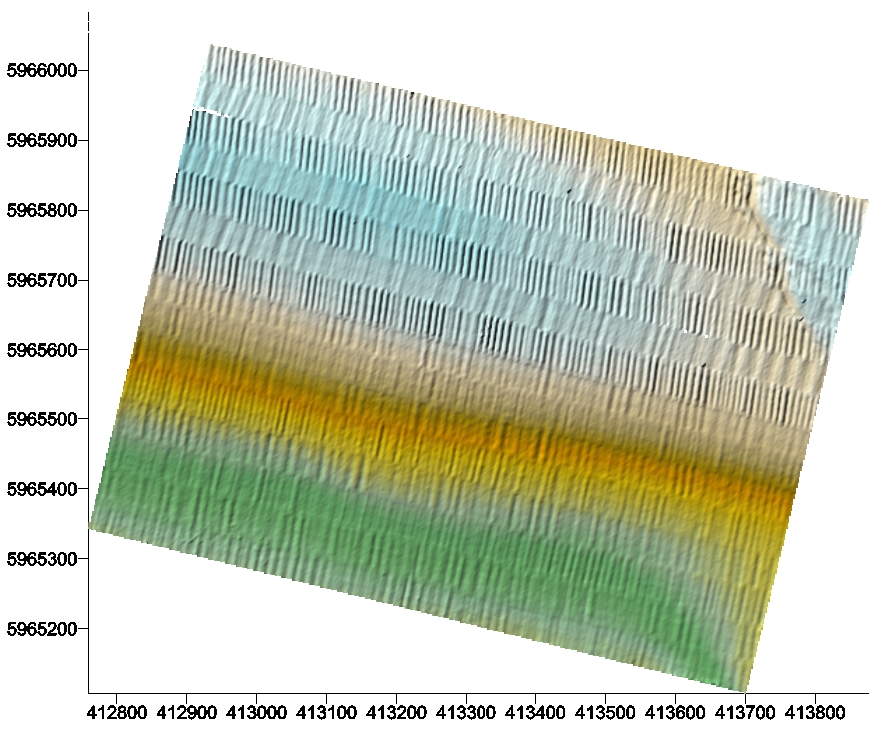
Ultrasound Measurements

and partly
DFG
(since 2004)
Analysis of uterine contractions and reconstruction of fetal brain activities
The University of Arkansas for Medical Sciences
(C. Lowery) and the University
of
Tübingen (H. Preissl) have
developed SQUID
(Superconducting Quantum Interference Device) which is a device for
prenatal diagnostics. With the help of this medical device one hopes to
understand and to identify pregnancies at risk.
The mathematical task is to develop methods that extract information about uterine contraction activities (by means of classification models) and to reconstruct the location and activity of the fetal brain activity.
The mathematical task is to develop methods that extract information about uterine contraction activities (by means of classification models) and to reconstruct the location and activity of the fetal brain activity.
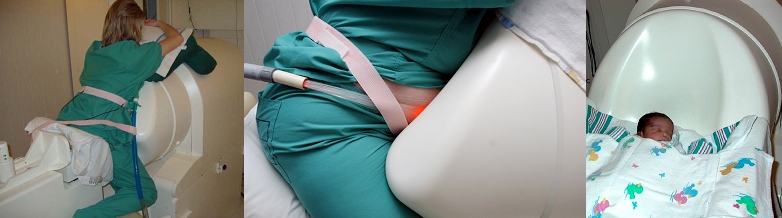
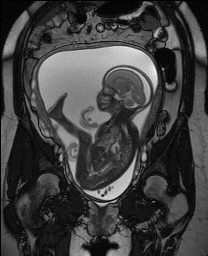
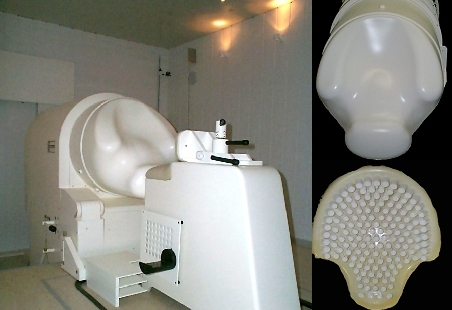
(since 2003)
Silex Systemi Integrati (F.
Gekat)
manufactures radar devices that analyze the lower atmosphere. The
overall goal is that weather radar systems should achieve an optimal
sampling (in time and space) of the atmosphere. However, the sampling
is limited by the range doppler dilemma (sampling range vs.
doppler frequency).
The focus is the development of methods to overcome the range doppler dilemma. To this end, an optimization of the pulse transmission technique and an efficient scheme to solve the resulting large system of equations need to be developed.
The focus is the development of methods to overcome the range doppler dilemma. To this end, an optimization of the pulse transmission technique and an efficient scheme to solve the resulting large system of equations need to be developed.

(2003-05)
The focus was
the construction of optimal
analyzing atoms (wavelets) that allow optimal representations of meteorological and medical data for further analysis. This project was done in collaboration with V. Lehmann (DWD-German Weather Agency) and H. Preissl
(MEG Zentrum, University Tübingen).
and partly DFG, HASSIP
(since 2002)
Iterative methods for linear (and nonlinear) operator equations with mixed sparsity and smoothness constraints
Operator
equations appear in several fields of
science and technology; typically given as an inverse and ill-posed
problem.
In
collaboration with
I. Daubechies
(Princeton University), L.
Vese
(UCLA-IPAM) and, moreover, with R. Ramlau (RICAM, Linz) and C. DeMol (ULB
Brussels) we develop iterative strategies for
inverse problems where the solution is assumed to have a particular
(possibly sparse) representation with respect to preassigned families
of frames. Typically the minimization of the inverse problem in its
variational form amounts to a (fixed point) iteration with a special
shrinkage operation applied in each step.
In the linear theory, typical examples are image deblurring, inversion of the Radon transform, image decomposition and restoration. The technology can also be applied to audio data coding. In the nonlinear theory one can attack the full nonlinear SPECT problem.
In the linear theory, typical examples are image deblurring, inversion of the Radon transform, image decomposition and restoration. The technology can also be applied to audio data coding. In the nonlinear theory one can attack the full nonlinear SPECT problem.



Simultaneously computed deblurred version, cartoon and texture component

(since 2002)
Wavelet-based regularisation methods for nonlinear diffusion equations
The most
important question in inverse problems
is to reconstruct a solution with the help of an observation. In this
project we consider the field of image processing, in particular
nonlinear diffusion equations. With the help special operator adapted
wavelet systems, we develop a numerical scheme to solve this special
nonlinear partial differential equation. This project is in
collaboration with J. Soares,
(Universidade Minho, Portugal).


Original and noisy image



A few steps of the iterative nonlinear smoothing

(2002-04)
Within the EU
Craft Program (Cooperative
Research Action For Technology) of the European Union SM-enterprises
are funded in order to develop with help of research institutes new and
innovative technologies. MEPROS (Meteorological profiling
system based on wavelet technology for radar and acoustic devices) was
a project to provide an analysis tool (software unit) that will provide
in the field of meteorology high quality measurements.
Meteorological stations,
airports (Frankfurt International Airport) or Off-Shore-Windparks will
have a significant benefit by MEPROS by receiving more accurate weather
data. To achieve such an impact, we have collaborated within an
impressive team of engineers, researchers and manufacturers: SHE AG
(Ludwigshafen, Germany), BIRAL (Bristol,
UK), Scintec AG
(Tübingen, Germany), Eurelettronica Icas Srl
(Rom, Italy), Espace
Eolien Developement (Lille, France), (Aveiro,
Protugal), Universidade de AveiroFH
Worms (Germany), ZETEM (Bremen,
Germany).
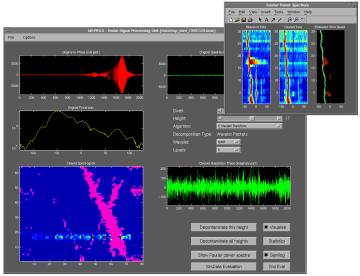
MEPROS Software Toolbox

(2002-03)
Wavelets in Banach-Spaces and Solving PDE's
The main goal
of the german-portugese cooperation
was
the analysis of wavelets in Banach spaces and its usage in solving
partial differential equations. We have developed strategies for
nonlinear elliptic problems. This project was
done in collaboration with U. Kähler and P.
Cerejeiras (Universidade de Aveiro, Portugal).
EU HASSIP
(since 2001)
As a participant within this project we have established a fruitful collaboration between several European research institutes. The focus is on (non-)harmonic analysis and its application in several fields of image and signal processing.
Together with S. Dahlke (University of Marburg), G. Steidl (University of Mannheim) and M. Fornasier (RICAM, Linz) we consider the construction of smoothness spaces (coorbit spaces)and the construction of Banach frames (to represent functions in them) . All this yields new insights when going beyond Hilbert spaces on the Euclidian plane, e.g. we are able to consider Gabor frame expansions on the sphere (or more general manifolds) and related nonlinear approximations.
(2001-03)
The focus was an
improvement of the modelling
and the analysis of radar echoes. In collaboration with the DWD-German Weather Agency (V.
Lehmann) and the GKSS-Research
Center Geesthacht (M. Quante) we
reconstruted
specific structures (e.g. fall traces of ice cristals) based on cloud
radar measurements.
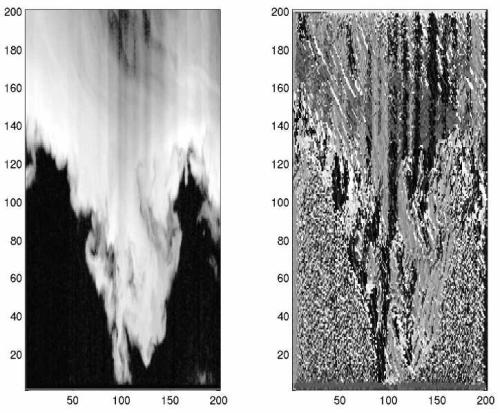
Reconstructed
cloud data and
extracted structures

(1999-00)
Analysis of X-Ray radiography images for an automatic detection of material errors
The IfG GmbH in Berlin-Adlershof has
developed new 2Dim-CCD-Cameras that were used for
testing the quality of two layered materials. The goal of this project
was the development of an algorithm that reconstructs the material
density automatically.

(1998)
since 1998
DWD, DFG
The goal of
this long lasting and very
fruitful collaboration with the DWD-German Weather Agency (V. Lehmann) is
the analysis of wind profiler radar data. Typically, wind profiler data
contain not only the clear air return but also contamination from
objects passing the radar beam. In order to identify atmospheric
informations, we focus on the modelling of clear air signals and
clutter components such echoes from migrating birds, airplanes or
surrounding objects such as wind turbines, digital video broadcast
(DVBT) or trees.
On the basis of advanced time-frequency methods such as wavelet frame and Gabor frame theory we have developed stochastic signal filtering procedures that allow an efficient and serious eleminination of the signal clutter components.Our latest state of the art procedure performs in average much better than all other methods on the "radar market" and is therefore implemented in the DWD's radar data processing unit.
On the basis of advanced time-frequency methods such as wavelet frame and Gabor frame theory we have developed stochastic signal filtering procedures that allow an efficient and serious eleminination of the signal clutter components.Our latest state of the art procedure performs in average much better than all other methods on the "radar market" and is therefore implemented in the DWD's radar data processing unit.